CONCEPTOS

¿Qué es didáctica?

Es el arte de enseñar. NERICI, (1969/1973) Considera que “la  didáctica está constituida por un conjunto de procedimientos y normas destinados  a dirigir  el aprendizaje  de la manera más eficiente posible.” Los docentes debemos reconocer los procedimientos y normas para la conducción de la enseñanza y el aprendizaje de los niños en la asignatura de matemática y en todas las asignaturas del programa curricular. Didáctica es el estudio de los elementos que interactúan en una situación de aprendizaje, para lograr los objetivos propuestos en la enseñanza aprendizaje.

En la didáctica las funciones de sus elementos, análisis y medios y recursos que hacen posible el acto didáctico con la aplicación de técnicas de realización y evaluación.

Además A.Pérez (1981) la define como ciencia y tecnología del sistema de comunicación intencional donde se desarrollan procesos de enseñnza aprendizaje en orden a optimizar principalmente, la formación intelectual.

También R. Medina  (1988) la define como el proceso de enseñanza aprendizaje  y la fundamentación del proyecto curricular que se lleva a cabo en una realidad específica, el aula en que se implementa, se aplica y se desarrolla el currículo.

X. Torres (1992) la define como la disciplina que estudia la praxis educativa proporcionando ayuda para reflexionar sobre la reconstrucción del conocimiento que tiene lugar en las instituciones escolares y para orientar los procesos de enseñanza aprendizaje, todo ello debe ser coherente  con una meta de orden  intelectual, social, moral, valiosa individual y socialmente.

Los autores coinciden en los procesos de enseñanza aprendizaje para el desarrollo curricular.

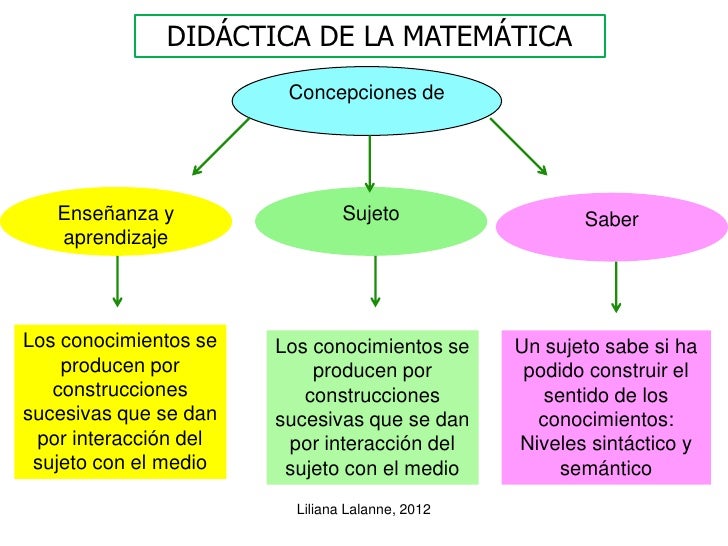
 DIDÁCTICA DE LA MATEMÁTICA                                  

1.    ¿Cuáles son los tres modelos de enseñanza que involucran la relación entre el docente, el alumno y el saber?

Primero el modelo llamado normativo, centrado en el saber donde el docente es quien aporta, comunica, ofrece y da ejemplos; el alumno debe imitar y aplicar al escuchar, retener, repetir lo que hace el docente.

El modelo llamado iniciativo, centrado en el alumno, el docente está atento a las necesidades e intereses del alumno, para que se sienta motivado.

El modelo llamado aproximativo centrado en la construcción del saber por el alumno, el docente parte de los conocimientos previos de los alumnos y diseña situaciones en las que deberán enfrentarse con obstáculos, que serán fuentes de nuevos conocimientos o les permitirán reestructurar los existentes (pensar, actuar, transformar). 

Se trata de herramientas de solución a los conocimientos que se pretende que el alumno construya.

2.    ¿Por qué se dice que enseñar matemática es equivalente a enseñar a resolver problemas, según Santaló?

Se dice que enseñar matemáticas, según Santaló es equivalente a enseñar a resolver problemas ya que se le ha llamado a la resolución de problemas el corazón de las matemáticas, es el verdadero sabor que atrae a los matemáticos de todas las épocas. El enfrentamiento con problemas adecuados que resulten motivadores, actitudes, hábitos, ideas para el desarrollo de herramientas apropiadas, en una palabra, la vida propia de las matemáticas.

Es necesario operar sobre la realidad con la participación de todos los miembros del grupo dispuestos a resolver ese problema preguntando, elaborando explicaciones, discutiendo propuestas, ofreciendo alternativas, planteando posibles soluciones. De ese modo, se tratarán ejes significativos en torno a los cuales se habrá de actuar para lograr un resultado cierto que luego el mismo grupo pondrán en práctica para verificar la calidad de lo resuelto.

Hay que partir del descubrimiento conjunto de las necesidades propias del grupo, para contribuir a los objetivos del aprendizaje, la situación propia de los grupos de investigación podrá lograr la necesaria ansiedad para resolverla. Es importante la función del docente  despertar en los alumnos la necesidad y el placer por intentar resolver situaciones matemáticas que surgen de las ideas de los niños  que no siempre son del marco de su realidad inmediata dentro de la escuela, sino también de su propia fantasía que es propio de la edad.

Las competencias suponen además de conocimiento o saberes, poder hacer.

Denominamos problema a toda situación que, enmarcada en las necesidades e intereses, pongan en conflicto al otro, le generen dudas, lo obligue a poner en marcha todos los conocimientos adquiridos pero insuficiente y lo estimule a reconocer las necesidades de adquirir nuevos contenidos transformados en saberes adquiridos.

Los problemas no tienen edades, sólo es necesario el conocimiento de la evolución de los alumnos para las formas que ellos requieren, los problemas pueden mantener su esencia, se plantea distintas formas de resolución adecuada al proceso cognitivo y, en consecuencia, las estrategias para solucionarlo, su eficacia y hasta el contenido mismo serán distintos.

Es bueno tener en cuenta que no hay problemas sino hay al menos dos soluciones que lleven a una misma respuesta. Existen tantas formas de resolución como el grupo encuentre, en la institución es necesaria una validación y una justificación suficiente ajustadas al rigor matemático propio de la edad y del niel de trabajo.

Otra consideración por parte del docente se relaciona con el uso del error: una solución o una simple propuesta pueden no ser las correctas, pero permitirá al docente iniciar un trabajo constructivo que conduzca a un resultado satisfactorio.

Tener un problema significa buscar conscientemente alguna acción apropiada para lograr un propósito claramente concebido, pero no inmediatamente alcanzable. Resolver un problema significa descubrir esa acción.

“Resolver problemas es el logro específico de la inteligencia, y la inteligencia es el don específico del hombre” (G. Polya)

Las ventajas de la enseñanza a través de la resolución de problemas son:

Ø  Manipule los objetos matemáticos;

Ø  active su propia capacidad mental;

Ø  ejercite su creatividad;

Ø  reflexione su propio proceso de pensamiento para mejorarlo conscientemente;

Ø  transfiera si fuera posible, estas actividades a otro aspecto de su trabajo mental;

Ø  adquiera confianza en sí mismo;

Ø  se divierta con su propia actividad mental;

Ø  se prepare para otros problemas de la ciencia y posiblemente, de su vida cotidiana;

Ø  se prepare para los nuevos retos de la tecnología y de la ciencia.

Metodología activa: basado en la experimentación por parte del alumno. Se centra en la actividad creadora del alumno, en su labor investigadora propia, en sus propios descubrimientos, porque entiende que es el propio alumno el que construye sus conocimientos.

Metodología heurística: enfatiza el dominio de los procedimientos (operaciones de pensamiento) y estrategias en contraposición con las que persiguen tácitamente la adquisición de contenidos como objetivo último.

Metodología diferenciada: Las dificultades para el aprendizaje difieren en gran medida de un alumno a otro. En esta metodología para guiarse en el diseño de actividades de aprendizaje mencionamos doce principios.  En condiciones iguales en donde una actividad es preferible a otra,

ü  si permite al alumno tomar decisiones razonables respecto a cómo desarrollarla y considerar las consecuencias de su elección.

ü  si atribuye al alumno un papel activo en su realización.

ü  si exige del alumno una investigación de ideas, procesos intelectuales, sucesos o fenómenos de orden personal o social, y lo estimulan a comprometerse con ella.

ü  si obliga al alumno a interactuar con la realidad.

ü  si puede ser realizada por el alumno de diversos niveles de capacidad y con intereses diferentes.

ü  si obliga al alumno a examinar, en un contexto nuevo, una idea, conceptos o ley que ya conoce.

ü  si obliga al alumno a examinar ideas o sucesos que normalmente son aceptados incondicionalmente por la sociedad.

ü  si coloca al alumno y al docente en una posición de éxito, fracaso o crítica.

ü  si obliga al alumno a reconsiderar y revisar sus esfuerzos iniciales.

ü  si obliga a aplicar y dominar reglas significativas, normas o disciplinas.

ü  si se ofrece al alumno la posibilidad de planificarlas con otros, participar en su desarrollo y comparar los resultados obtenidos.

ü  si es relevante para los propósitos e intereses explícitos de los alumnos.